 |
О ВОЗМОЖНОЙ НЕУСТОЙЧИВОСТИ ТЕПЛОВОГО БАЛАНСА ЗЕМЛИ
Глобальное потепление — одна из проблем, привлекающих наибольшее внимание общества.
В ее обсуждении активно участвуют не только исследователи, но также журналисты
и политики. Можно считать установленным, что потепление связано с ростом концентрации
в атмосфере «парниковых» газов, и др. Что касается причин этого роста,
то относительная роль антропогенных и естественных факторов пока не ясна. Мы хотим
обратить внимание на некоторые особенности кривых «среднегодовая температура (T)
— время (t)», построенных по данным метеорологических наблюдений. Данные
имеются примерно за 100 последних лет. На сглаженном графике T(t) видна точка перегиба,
рост идет сначала с замедлением, а затем (последние ~50 лет) — с нарастающим ускорением.
Чтобы пояснить, почему такое поведение может оказаться важным, рассмотрим простое уравнение
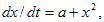 |
(1) |
где x — величина, зависящая от времени, a — постоянный параметр.
При a<0 имеются стационарные точки
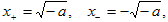 |
(2) |
точка x- устойчива, а x+ неустойчива. Если же a>0,
стационарных решений нет, производная dx/dt всегда положительна, x возрастает.
Пусть в начальный момент t=0, x=x0 времени. Тогда
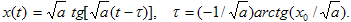 |
(3) |
При x0<0 на графике x(t) есть точка перегиба
t=t, x=0. Чем меньше a тем длительнее стадия медленного
роста около этой точки. Но в конце концов неустойчивость развивается, x нарастает все быстрее.
Конечно, качественное сходство функции x(t) и сглаженной температурной зависимости для земной
атмосферы (см. рис.1) ни в малейшей степени не является доказательным: математическая модель,
описывающая тепловой баланс нашей планеты, несравненно сложнее уравнения (1). Однако, поведение,
подобное решению (3) и рис.1, характерно для так называемой взрывной неустойчивости вблизи порога
ее развития (т.е., при малой надкритичности). Если в качестве математической модели используется
система обыкновенных дифференциальных уравнений вида
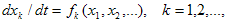 |
(4) |
то в фазовом пространстве этой системы устойчивую стационарную точку окружает некоторый бассейн
притяжения. Взрывная неустойчивость развивается, когда к стационарной точке подходит какой-либо участок
границы бассейна. Пусть направлению подхода отвечает ось xi в фазовом пространстве.
Тогда xi подчиняется уравнению типа (1), а порогу неустойчивости отвечает обращение
параметра ai в нуль. Например, ai может быть
пропорционально разности между концентрацией парниковых газов и ее критическим значением, а
xi — отклонению усредненной температуры от значения в точке перегиба.
К примерам взрывной неустойчивости относятся: пробой диэлектриков, разрушение материала при
критической величине нагрузки, жесткое возбуждение автоколебаний, затухание волн реакции при пороговой
величине потерь и др. явления. Уравнение (1) вводилось также при описании перехода от ламинарного течения
к турбулентному через перемежаемость. Стационарный режим, параметры которого близки к границе
неустойчивости (не только взрывной), обладает высокой восприимчивостью. Можно сказать, что мала
«сила», возвращающая систему в стационарное состояние после отклонения от него. Поэтому
отклонения возникают легко и релаксируют медленно. Слабый «шум», присущий всякой реальной
системе, соответственно, усиливается, в наибольшей степени усиливаются его низкочастотные составляющие.
По нарастанию мягких мод в спектре флуктуаций можно, в принципе, судить о приближении «катастрофы»
данного стационарного режима. Так в случае уравнения (1) вещественная и мнимая части восприимчивости
на частоте w равны
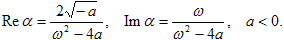 |
(5) |
При | a | → 0 восприимчивость расходится на низких частотах.
Для нестационарных решений уравнения (1), описывающих развитие неустойчивости при a>0 такое
определение восприимчивости непригодно. Однако, легко видеть, что с ростом x должны расти
и флуктуации. Действительно, добавляя в правую часть (1) малое слагаемое y(t) находим, что
возмущение функции x(t) из (3) равно
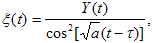 |
(6) |
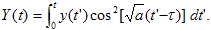 |
(7) |
Начальное значение возмущения в (6) принято равным нулю. Если y(t) — случайная функция,
то и Y(t) будет случайной функцией, причем нет оснований ожидать, что дисперсия
<Y2> будет много меньше <y2>. Следовательно, размах
флуктуаций 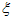 на стадии роста x после точки перегиба велик по сравнению
с y так как знаменатель в (6) уменьшается с t, обращаясь в нуль при на стадии роста x после точки перегиба велик по сравнению
с y так как знаменатель в (6) уменьшается с t, обращаясь в нуль при 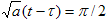 .
Абсолютная величина отклонений от сглаженной кривой (рис.1) показаны на рис.2. График хаотичен,
как и сами отклонения, но «в среднем» дисперсия год от года растет после того, как пройдена
точка перегиба на рис.1. .
Абсолютная величина отклонений от сглаженной кривой (рис.1) показаны на рис.2. График хаотичен,
как и сами отклонения, но «в среднем» дисперсия год от года растет после того, как пройдена
точка перегиба на рис.1.
Именно эти две особенности хода температуры — точка перегиба на сглаженной кривой и рост
хаотических отклонений после этой точки — заставляют, по нашему мнению, отнестись серьезно
к предположению о взрывной неустойчивости теплового баланса. Чтобы проверить это предположение,
нужно записать систему балансовых уравнений (уравнений макроскопической кинетики) для температуры
и концентраций атмосферных компонентов. Затем предстоят анализ и численные эксперименты с этими
уравнениями. В их структуре должны быть учтены все существенные обратные связи, способные порождать
неустойчивость. Очевидный пример такой связи — обмен диоксида углерода между почвой и воздухом.
Чем выше температура воздуха, тем интенсивнее выход диоксида из почвы, что, в свою очередь, ведет
к повышению температуры.
Для записи макрокинетических уравнений необходимы данные из разных областей, включая биологию
и геологию. Их могут предоставить соответствующие специалисты. В работе с полученными уравнениями
большую роль могут сыграть математики, специалисты по численным методам. Но координаторами всей программы
должны выступать физики, так как построение математических моделей — специальность физика-теоретика.
Если мы действительно наблюдаем развитие взрывной неустойчивости, то только макрокинетические уравнения
могут ответить на вопрос: каков будет новый установившийся режим? Всевозможные климатологические
экстраполяции здесь непригодны. Не исключено, что время для исследований упущено, во всяком случае,
его остается совсем немного.
Программа, предусмотренная Киотским протоколом требует грандиозных затрат — около 5 трлн. долл.
Средства эти расходуются, в значительной мере, вслепую, без достаточного научного обоснования. Польза
от ограничения хозяйственных выбросов не очевидна, если это не касается веществ, заведомо вредных для
здоровья. Диоксид углерода к таким веществам не относится. Наша точка зрения: необходимо сосредоточить
силы (лучше всего, в виде нескольких независимых групп) на макрокинетических уравнениях, о которых
сказано выше, чтобы получить быстрый и, по возможности, точный ответ — как будет в дальнейшем
меняться земная температура. Только знание этого ответа может сделать действия мирового сообщества
эффективными. Задача организации исследовательских групп, обеспечения их работы является важной
и срочной. Именно в этом мы хотим убедить сейчас и исследователей, и общественность.
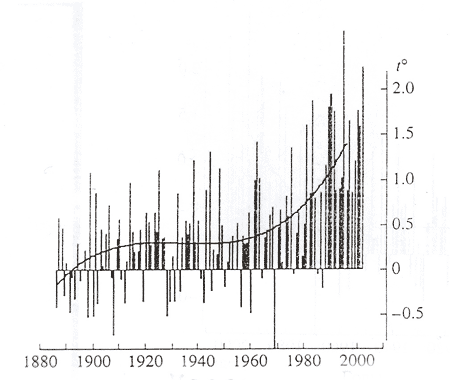
Рис.1. Температура воздуха над Россией (из Доклада Ю. А. Осипова. Вестник АН, № 10, 2004).
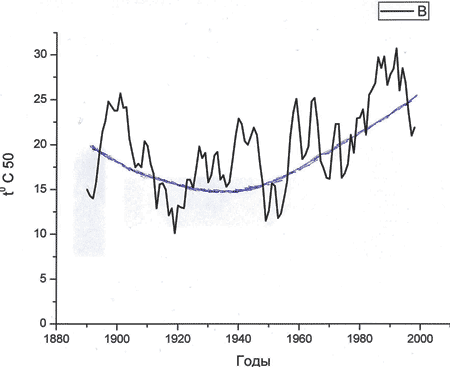
Рис.2. Отклонения от сглаженной кривой, показанной на рис.1.
|










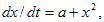
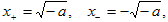
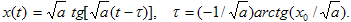
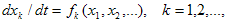
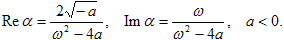
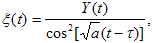
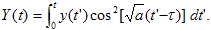
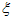 на стадии роста x после точки перегиба велик по сравнению
с y так как знаменатель в (6) уменьшается с t, обращаясь в нуль при
на стадии роста x после точки перегиба велик по сравнению
с y так как знаменатель в (6) уменьшается с t, обращаясь в нуль при 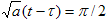 .
Абсолютная величина отклонений от сглаженной кривой (рис.1) показаны на рис.2. График хаотичен,
как и сами отклонения, но «в среднем» дисперсия год от года растет после того, как пройдена
точка перегиба на рис.1.
.
Абсолютная величина отклонений от сглаженной кривой (рис.1) показаны на рис.2. График хаотичен,
как и сами отклонения, но «в среднем» дисперсия год от года растет после того, как пройдена
точка перегиба на рис.1.

